This is a rough draft for some possible contributions to the article on free groups. |

In mathematics, a free group is a group whose generators satisfy no relations, other than those that follow from the group axioms. Specifically, a group F is free over a generating set S if every element of F can be expressed uniquely as a reduced word in the elements of S. Free groups are closely related to the theory of group presentations, and they play an important role in algebraic topology and geometric group theory.
History edit
Moved to article |
Elementary properties edit
Construction edit
Moved to article |
Universal property edit
Moved to article |
Rank edit
The rank of a free group is the cardinality of the free generating set. Two free groups with the same rank are isomorphic, so it makes sense to talk about "the free group of rank n", denoted Fn.
From this point of view, there is a single infinite family of finitely generated free groups:
The first free group F1 is just the infinite cyclic group. The remaining free groups are all nonabelian, and no two are isomorphic.
There are also free groups of infinite rank. The free group with countable rank is usually denoted F∞ or Fω. Larger free groups are denoted Fα, where α is an infinite cardinal.
Free groups and presentations edit
If S is a generating set for a group G, the inclusion S → G defines a homomorphism π: FS → G. The image under π of an element of FS is the product of the reduced word inside of G. The homomorphism π is onto, making G a quotient of FS:
Thus every group is the quotient of a free group.
Interpretation of relations edit
In general, a relation in G is a pair of reduced words whose products are equal. For example, the permutations a = (1 2 3) and b = (1 2) in the symmetric group Sym(3) satisfy the relations
The kernel of π consists of all words in FS that equal the identity in G. These correspond to relations of the form ω = 1. Any relation in G can be written in this form:
Thus any relation in G corresponds to some element of ker(π). For this reason, the kernel of π is known as the group of relations for G.
Defining relations edit
A presentation for a group G is a pair ⟨S | R⟩, where S is a generating set for G, and R is a set of defining relations. That is, R is a set of relations in G with the property that every relation in G can be deduced from those in R.
Given a subset R of ker(π), the relations that can be deduced from those in R are precisely the elements of the normal closure of R in FS. (The normal closure is the subgroup of FS generated by all conjugates of elements of R, i.e. the smallest normal subgroup of FS containing R.) The relations in R define G if and only if the normal closure of R is all of FS.
Example edit
Consider the group Z × Z, generated by the elements a = (1,0) and b = (0,1). This group has presentation
Let F2 be the free group generated by a and b. Becuase ab = ba in Z × Z, the commutator aba-1b-1 lies in the kernel of the homomorphism π: F2 → Z × Z. In fact, the kernel of π is the normal closure of this element, which is precisely the commutator subgroup of F2.
Algebraic properties edit
Free generating sets edit
The free generating set for a free group is not unique. For example, if F2 is the free group generated by {a, b}, then {a, b-1} is also a free generating set, as is {a, ab}. All free generating sets for a free group F have the same cardinality, namely the rank of F. Conversely, any n elements of Fn that generate Fn are necessarily a free generating set. This is related to the fact that Fn is Hopfian (every homomorphism from Fn onto itself is an isomorphism).
Given a free generating set {a1, ..., an} for Fn, a Nielsen move is one of the following operations:
- For some i, replace ai by ai-1.
- For some i ≠ j, replace ai by aiaj or ajai.
(These are analogous to elementary row operations for matrices.) The result of a Nielsen move is another free generating set for Fn. This allows for the construction of relatively complicated free generating sets:
Any two free generating sets for Fn differ by a sequence of Nielsen moves.
Automorphisms edit
If S is a free generating set for F, then a homomorphism φ: F → F is an automorphism if and only if φ(S) is another free generating set. For example,
defines an automorphism of F2. The automorphisms of free groups have been studied extensively, and the geometry of Out(Fn) is an important subject of research in geometric group theory.
Subgroups edit
Every subgroup of a free group is free. This is the famous Nielsen-Schreier theorem, first proven by Nielsen for finitely-generated subgroups, and then extended to the general case by Schreier. (Max Dehn was the first to prove the general case, but he did not publish his result.)
The simplest proof of the Nielsen-Schreier theorem uses fundamental group and covering spaces (see below). Paradoxically, the rank of a subgroup of a free group F is usually greater than the rank of F.
The remainder of this draft is in very rough form. In my opinion, the second half of the article should cover some or all of the following topics:
|
Conjugacy, roots, and centralizers edit
There is a simple solution to the conjugacy problem in a free group.
Topology edit
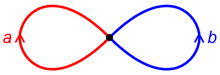
The free group FS can be interpreted as the fundamental group of a rose, with one petal for each element of S. For example, the element aba-1 in F2 corresponds to the path in the rose that goes forwards around a, forwards around b, and then backwards around a.
The Cayley graph of Fn is an infinite tree (see the picture at the beginning of the article), which can be interpreted as the universal cover of the associated rose. In general, the universal cover of any presentation complex for a group is a Cayley complex.
Fundamental group of a graph edit
The fundamental group of any topological graph is free. In particular, given a connected graph Γ, choose a spanning tree T. Then the quotient map Γ → Γ / T is a homotopy equivalence, and Γ / T is homeomorphic to a rose.
If Γ is finite with v vertices and e edges, then T must have v – 1 edges, so the fundamental group of Γ is free of rank e – v + 1. When Γ is planar, this is the same as the number of interior regions.
Given a basepoint p ∈ T, an explicit free basis for π1(Γ, p) can be described as follows. Let E be the set of edges of Γ that do not lie in T, and choose an orientation for each edge in E. For each e ∈ E, let αe be a path that travels in T from p to the beginning of e, travels along e, and then travels in T back to p. Then the loops {αe | e ∈ E} are a free basis for π1(Γ, p).
Subgroups edit
Cohomology edit
Because the universal cover of a rose is contractible, the rose is an Eilenberg-MacLane space for the corresponding free group. In particular, the group cohomology of a free group F is the same as the cohomology of the associated rose. It follows that Hn(F) = 0 for all n ≥ 2, so every free group has cohomological dimension one. John Stallings and Richard Swan have shown that any group with cohomological dimension one is free[1][2]. One interesting consequence is that any torsion-free virtually free group is free.
Geometry edit

Finitely generated free groups play an important role in geometric group theory.
Action on the hyperbolic plane edit
There is a simple action of F2 on the hyperbolic plane, shown in the figure to the right. This figure shows an embedding of the Cayley graph of F2 in the hyperbolic plane, which is dual to a tiling of the plane by ideal quadrilaterals. The action of F2 on its Cayley graph extends to an isometric action of F2 on the hyperbolic plane.
Further properties edit
- Finitely-generated free groups are Hopfian. That is, any homomorphism from Fn onto itself is an automorphism.
- Stallings and Swan have shown that any group with cohomological dimension one is free.
- The free product of Fm and Fn is Fm+n. In particular, every free group is the free product of infinite cyclic groups. A free factor of a free group F is a subgroup H such that F = H ∗ K for some subgroup K.
- Free groups are residually finite. That is, given any nontrivial element ω of a free group F, there exists a finite group G and a homomorphism φ: F → G such that φ(ω) ≠ 1.
General properties edit
The free group F2 contains each of F3, F4, ... as a subgroup of finite index. It follows that the groups F2, F3, ... are all quasi-isometric. For this reason, the study of the geometry of free groups focuses on F2.
What follows is a list of facts copied directly from some references. I have yet to sort through the list. |
Stuff from Baumslag edit
- There is no algorithm to decide whether a given group is free. (This is because freeness is a Markov property.)
- Finitely generated free groups are hopfian. That is, no proper quotient of Fn is isomorphic with Fn.
- There are some other important developments in the study of Combinatorial Group Theory.
These include the so-called Bass-Serre theory of groups acting on trees (see Chapter VII), the cohomology of groups, in particular the extraordinary proof by Stallings and Swan that groups of cohomological dimension one are free (J.R. Stallings: Group Theory and 3-dimensional Manifold, Yale Monographs 4 (1971) and the graph-theoretic methods of Stallings with applications by Gersten to the automorphisms of free groups, yielding for example his ¯xed point theorem of 1984 (S.M. Gersten: On Fixed Points of Certain Automorphisms of Free Groups, Proc. London Math. Soc. 48 (1984), 72-94)
- Let F be a finitely generated free group. Then the fixed set of any automorphism of F is finitely generated.
- A torsion-free virtually free group is free. (Consequence of the theorem of Stallings and Swan.)
- Let H be a finitely generated subgroup of a finitely generated free group F. Then H is virtually a free factor of F.
- Free factors of a free group are never normal.
- (Schreier) If H is a finitely generated normal subgroup of a free group F, then
either H = 1 or H is of finite index in F (and so F is finitely generated).
- (F.W. Levi) Free groups are residually finite.
- (J. Nielsen 1918) Let F be a free group of finite rank n. Suppose F is generated
by some set X of n elements. Then X freely generates F. (Follows from hopfian)
- If A * B is free, then so are A and B.
- Tits alternative
- B. Baumslag & S.J. Pride (J. London Math. Soc. (2) 17 (1978), 425-426). Let G be a group given by m+1 generators and n relations (m; n < 1). If
(m + 1) ¡ n ¸ 2 then G contains a subgroup of ¯nite index which maps onto a free group of rank two.
- Theorem 7 (W. Magnus 1932) Let
G = h a1; : : : ; am ; r = 1 i be a group de¯ned by a single relation. Suppose r is cyclically reduced and involves the generator a1. Then gp(a2; : : : ; am) is a free subgroup of G freely generated by a2; : : : ; am. Theorem 7 is sometimes referred to as the Freiheitssatz.
- A group G is said to act freely on a tree if it acts without inversion and
only the identity element leaves either a vertex or an edge invariant. Let G act freely on a tree. Then G is free.
Stuff from Bowditch edit
- Any hyperbolic group that is not finite or virtually cyclic contains a free subgroup of
rank 2, and hence free subgroups of any countable rank.
- Sela characterises groups with the same first order theory as free groups as “limit groups”.
More edit
- Theorem 5.2 (Howson) The intersection of two finitely generated subgroups
of a free group is again finitely generated.
Volume growth edit
Free groups have exponential growth. The growth function for Fn is given by:
Dimension edit
Free groups have cohomological dimension one. Stallings' theorem states that any group with virtual cohomological dimension 1 is a free group.
Amenability edit
Free groups are central to the study of amenability. The free group F2 is not amenable, as it exhibits a simple paradoxical decomposition. This decomposition plays an important role in the proof of the Banach-Tarski paradox.
It was conjectured that a group is non-amenable if and only if it contains a copy of F2. This conjecture was disproven (FIND MORE INFORMATION)
Notes edit
- ^ Stallings, John R. (September 1968). "On torsion-free groups with infinitely many ends". Annals of Mathematics, 2nd Ser. 88 (2): 312–334.
- ^ Swan, Richard G. (August 1969). "Groups of cohomological dimension one". Journal of Algebra. 12 (4): 585–610. doi:10.1016/0021-8693(69)90030-1.
References edit
- Hatcher, Allen (2002). Algebraic topology. Cambridge, UK: Cambridge University Press. ISBN 0-521-79540-0.
- Schupp, Paul E.; Lyndon, Roger C. (2001). Combinatorial group theory. Berlin: Springer. ISBN 3-540-41158-5.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Solitar, Donald; Magnus, Wilhelm; Karrass, Abraham (2004). Combinatorial group theory: presentations of groups in terms of generators and relations. New York: Dover Publications. ISBN 0-486-43830-9.
{{cite book}}: CS1 maint: multiple names: authors list (link) - Stillwell, John (1993). Classical topology and combinatorial group theory. Berlin: Springer-Verlag. ISBN 0-387-97970-0.







