Virtual displacement

In analytical mechanics, a branch of applied mathematics and physics, a virtual displacement (or infinitesimal variation) $\delta \gamma$ shows how the mechanical system's trajectory can hypothetically (hence the term virtual) deviate very slightly from the actual trajectory $\gamma$ of the system without violating the system's constraints. For every time instant $t,$ $\delta \gamma (t)$ is a vector tangential to the configuration space at the point $\gamma (t).$ The vectors $\delta \gamma (t)$ show the directions in which $\gamma (t)$ can "go" without breaking the constraints.

One degree of freedom.

Two degrees of freedom.

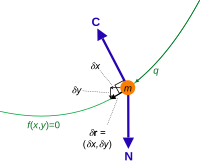
Constraint force C and virtual displacement δr for a particle of mass m confined to a curve. The resultant non-constraint force is N. The components of virtual displacement are related by a constraint equation.

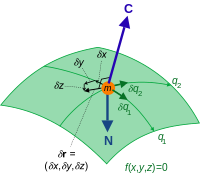
For example, the virtual displacements of the system consisting of a single particle on a two-dimensional surface fill up the entire tangent plane, assuming there are no additional constraints.

If, however, the constraints require that all the trajectories $\gamma$ pass through the given point $\mathbf {q}$ at the given time $\tau ,$ i.e. $\gamma (\tau )=\mathbf {q} ,$ then $\delta \gamma (\tau )=0.$

Notations

Let $M$ be the configuration space of the mechanical system, $t_{0},t_{1}\in \mathbb {R}$ be time instants, $q_{0},q_{1}\in M,$ $C^{\infty }[t_{0},t_{1}]$ consists of smooth functions on $[t_{0},t_{1}]$, and

$P(M)=\{\gamma \in C^{\infty }([t_{0},t_{1}],M)\mid \gamma (t_{0})=q_{0},\ \gamma (t_{1})=q_{1}\}.$

The constraints $\gamma (t_{0})=q_{0},$ $\gamma (t_{1})=q_{1}$ are here for illustration only. In practice, for each individual system, an individual set of constraints is required.

Definition

For each path $\gamma \in P(M)$ and $\epsilon _{0}>0,$ a variation of $\gamma$ is a function $\Gamma :[t_{0},t_{1}]\times [-\epsilon _{0},\epsilon _{0}]\to M$ such that, for every $\epsilon \in [-\epsilon _{0},\epsilon _{0}],$ $\Gamma (\cdot ,\epsilon )\in P(M)$ and $\Gamma (t,0)=\gamma (t).$ The virtual displacement $\delta \gamma :[t_{0},t_{1}]\to TM$ $(TM$ being the tangent bundle of $M)$ corresponding to the variation $\Gamma$ assigns to every $t\in [t_{0},t_{1}]$ the tangent vector

$\delta \gamma (t)={\frac {d\Gamma (t,\epsilon )}{d\epsilon }}{\Biggl |}_{\epsilon =0}\in T_{\gamma (t)}M.$

In terms of the tangent map,

$\delta \gamma (t)=\Gamma _{*}^{t}\left({\frac {d}{d\epsilon }}{\Biggl |}_{\epsilon =0}\right).$

Here $\Gamma _{*}^{t}:T_{0}[-\epsilon ,\epsilon ]\to T_{\Gamma (t,0)}M=T_{\gamma (t)}M$ is the tangent map of $\Gamma ^{t}:[-\epsilon ,\epsilon ]\to M,$ where $\Gamma ^{t}(\epsilon )=\Gamma (t,\epsilon ),$ and $\textstyle {\frac {d}{d\epsilon }}{\Bigl |}_{\epsilon =0}\in T_{0}[-\epsilon ,\epsilon ].$

Properties

• Coordinate representation. If $\{q_{i}\}_{i=1}^{n}$ are the coordinates in an arbitrary chart on $M$ and $n=\mathop {\rm {dim}} M,$ then

$\delta \gamma (t)=\sum _{i=1}^{n}{\frac {d[q_{i}(\Gamma (t,\epsilon ))]}{d\epsilon }}{\Biggl |}_{\epsilon =0}\cdot {\frac {d}{dq_{i}}}{\Biggl |}_{\gamma (t)}.$

• If, for some time instant $\tau$ and every $\gamma \in P(M),$ $\gamma (\tau )={\text{const}},$ then, for every $\gamma \in P(M),$ $\delta \gamma (\tau )=0.$

• If $\textstyle \gamma ,{\frac {d\gamma }{dt}}\in P(M),$ then $\delta {\frac {d\gamma }{dt}}={\frac {d}{dt}}\delta \gamma .$

Examples

Free particle in R³

A single particle freely moving in $\mathbb {R} ^{3}$ has 3 degrees of freedom. The configuration space is $M=\mathbb {R} ^{3},$ and $P(M)=C^{\infty }([t_{0},t_{1}],M).$ For every path $\gamma \in P(M)$ and a variation $\Gamma (t,\epsilon )$ of $\gamma ,$ there exists a unique $\sigma \in T_{0}\mathbb {R} ^{3}$ such that $\Gamma (t,\epsilon )=\gamma (t)+\sigma (t)\epsilon +o(\epsilon ),$ as $\epsilon \to 0.$ By the definition,

$\delta \gamma (t)=\left({\frac {d}{d\epsilon }}{\Bigl (}\gamma (t)+\sigma (t)\epsilon +o(\epsilon ){\Bigr )}\right){\Biggl |}_{\epsilon =0}$

which leads to

$\delta \gamma (t)=\sigma (t)\in T_{\gamma (t)}\mathbb {R} ^{3}.$

Free particles on a surface

$N$ particles moving freely on a two-dimensional surface $S\subset \mathbb {R} ^{3}$ have $2N$ degree of freedom. The configuration space here is

$M=\{(\mathbf {r} _{1},\ldots ,\mathbf {r} _{N})\in \mathbb {R} ^{3\,N}\mid \mathbf {r} _{i}\in \mathbb {R} ^{3};\ \mathbf {r} _{i}\neq \mathbf {r} _{j}\ {\text{if}}\ i\neq j\},$

where $\mathbf {r} _{i}\in \mathbb {R} ^{3}$ is the radius vector of the $i^{\text{th}}$ particle. It follows that

$T_{(\mathbf {r} _{1},\ldots ,\mathbf {r} _{N})}M=T_{\mathbf {r} _{1}}S\oplus \ldots \oplus T_{\mathbf {r} _{N}}S,$

and every path $\gamma \in P(M)$ may be described using the radius vectors $\mathbf {r} _{i}$ of each individual particle, i.e.

$\gamma (t)=(\mathbf {r} _{1}(t),\ldots ,\mathbf {r} _{N}(t)).$

This implies that, for every $\delta \gamma (t)\in T_{(\mathbf {r} _{1}(t),\ldots ,\mathbf {r} _{N}(t))}M,$

$\delta \gamma (t)=\delta \mathbf {r} _{1}(t)\oplus \ldots \oplus \delta \mathbf {r} _{N}(t),$

where $\delta \mathbf {r} _{i}(t)\in T_{\mathbf {r} _{i}(t)}S.$ Some authors express this as

$\delta \gamma =(\delta \mathbf {r} _{1},\ldots ,\delta \mathbf {r} _{N}).$

Rigid body rotating around fixed point

A rigid body rotating around a fixed point with no additional constraints has 3 degrees of freedom. The configuration space here is $M=SO(3),$ the special orthogonal group of dimension 3 (otherwise known as 3D rotation group), and $P(M)=C^{\infty }([t_{0},t_{1}],M).$ We use the standard notation ${\mathfrak {so}}(3)$ to refer to the three-dimensional linear space of all skew-symmetric three-dimensional matrices. The exponential map $\exp :{\mathfrak {so}}(3)\to SO(3)$ guarantees the existence of $\epsilon _{0}>0$ such that, for every path $\gamma \in P(M),$ its variation $\Gamma (t,\epsilon ),$ and $t\in [t_{0},t_{1}],$ there is a unique path $\Theta ^{t}\in C^{\infty }([-\epsilon _{0},\epsilon _{0}],{\mathfrak {so}}(3))$ such that $\Theta ^{t}(0)=0$ and, for every $\epsilon \in [-\epsilon _{0},\epsilon _{0}],$ $\Gamma (t,\epsilon )=\gamma (t)\exp(\Theta ^{t}(\epsilon )).$ By the definition,

$\delta \gamma (t)=\left({\frac {d}{d\epsilon }}{\Bigl (}\gamma (t)\exp(\Theta ^{t}(\epsilon )){\Bigr )}\right){\Biggl |}_{\epsilon =0}=\gamma (t){\frac {d\Theta ^{t}(\epsilon )}{d\epsilon }}{\Biggl |}_{\epsilon =0}.$

Since, for some function $\sigma :[t_{0},t_{1}]\to {\mathfrak {so}}(3),$ $\Theta ^{t}(\epsilon )=\epsilon \sigma (t)+o(\epsilon )$, as $\epsilon \to 0$,

$\delta \gamma (t)=\gamma (t)\sigma (t)\in T_{\gamma (t)}SO(3).$

See also

• D'Alembert principle
• Virtual work