Picture of the month
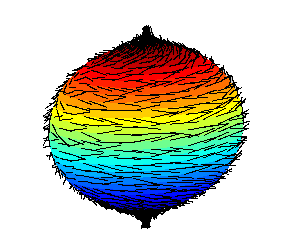
Illustration of a failed attempt to comb the "hair" on a ball flat, leaving a tuft sticking out at each pole. The hairy ball theorem of algebraic topology proves that whenever one attempts to comb a hairy ball flat, there will always be at least one tuft of hair at one point on the ball. More precisely, it states that there is no nonvanishing continuous tangent-vector field on an even-dimensional n‑sphere (an ordinary sphere in three-dimensional space is known as a "2-sphere"). This is not true of certain other three-dimensional shapes, such as a torus (doughnut shape) which can be combed flat. The theorem was first stated by Henri Poincaré in the late 19th century, and first proved in 1912 by L. E. J. Brouwer. If one idealizes the wind in the Earth's atmosphere as a tangent-vector field, then the hairy ball theorem implies that given any wind at all on the surface of the Earth, there must at all times be a cyclone somewhere. Note, however, that wind can move vertically in the atmosphere, so the idealized case is not meteorologically sound.
| ...Archive | Read more... |