B6 polytope

Orthographic projections in the B₆ Coxeter plane

6-cube

6-orthoplex

6-demicube

In 6-dimensional geometry, there are 64 uniform polytopes with B₆ symmetry. There are two regular forms, the 6-orthoplex, and 6-cube with 12 and 64 vertices respectively. The 6-demicube is added with half the symmetry.

They can be visualized as symmetric orthographic projections in Coxeter planes of the B₆ Coxeter group, and other subgroups.

Graphs

Symmetric orthographic projections of these 64 polytopes can be made in the B₆, B₅, B₄, B₃, B₂, A₅, A₃, Coxeter planes. A_k has [k+1] symmetry, and B_k has [2k] symmetry.

These 64 polytopes are each shown in these 8 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.

#	Coxeter plane graphs							Coxeter-Dynkin diagram Schläfli symbol Names
	B6 [12]	B5 / D4 / A4 [10]	B4 [8]	B3 / A2 [6]	B2 [4]	A5 [6]	A3 [4]
1								{3,3,3,3,4} 6-orthoplex Hexacontatetrapeton (gee)
2								t1{3,3,3,3,4} Rectified 6-orthoplex Rectified hexacontatetrapeton (rag)
3								t2{3,3,3,3,4} Birectified 6-orthoplex Birectified hexacontatetrapeton (brag)
4								t2{4,3,3,3,3} Birectified 6-cube Birectified hexeract (brox)
5								t1{4,3,3,3,3} Rectified 6-cube Rectified hexeract (rax)
6		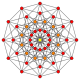						{4,3,3,3,3} 6-cube Hexeract (ax)
64								h{4,3,3,3,3} 6-demicube Hemihexeract
7								t0,1{3,3,3,3,4} Truncated 6-orthoplex Truncated hexacontatetrapeton (tag)
8								t0,2{3,3,3,3,4} Cantellated 6-orthoplex Small rhombated hexacontatetrapeton (srog)
9								t1,2{3,3,3,3,4} Bitruncated 6-orthoplex Bitruncated hexacontatetrapeton (botag)
10								t0,3{3,3,3,3,4} Runcinated 6-orthoplex Small prismated hexacontatetrapeton (spog)
11								t1,3{3,3,3,3,4} Bicantellated 6-orthoplex Small birhombated hexacontatetrapeton (siborg)
12								t2,3{4,3,3,3,3} Tritruncated 6-cube Hexeractihexacontitetrapeton (xog)
13								t0,4{3,3,3,3,4} Stericated 6-orthoplex Small cellated hexacontatetrapeton (scag)
14								t1,4{4,3,3,3,3} Biruncinated 6-cube Small biprismato-hexeractihexacontitetrapeton (sobpoxog)
15								t1,3{4,3,3,3,3} Bicantellated 6-cube Small birhombated hexeract (saborx)
16								t1,2{4,3,3,3,3} Bitruncated 6-cube Bitruncated hexeract (botox)
17								t0,5{4,3,3,3,3} Pentellated 6-cube Small teri-hexeractihexacontitetrapeton (stoxog)
18								t0,4{4,3,3,3,3} Stericated 6-cube Small cellated hexeract (scox)
19								t0,3{4,3,3,3,3} Runcinated 6-cube Small prismated hexeract (spox)
20								t0,2{4,3,3,3,3} Cantellated 6-cube Small rhombated hexeract (srox)
21								t0,1{4,3,3,3,3} Truncated 6-cube Truncated hexeract (tox)
22								t0,1,2{3,3,3,3,4} Cantitruncated 6-orthoplex Great rhombated hexacontatetrapeton (grog)
23								t0,1,3{3,3,3,3,4} Runcitruncated 6-orthoplex Prismatotruncated hexacontatetrapeton (potag)
24								t0,2,3{3,3,3,3,4} Runcicantellated 6-orthoplex Prismatorhombated hexacontatetrapeton (prog)
25								t1,2,3{3,3,3,3,4} Bicantitruncated 6-orthoplex Great birhombated hexacontatetrapeton (gaborg)
26								t0,1,4{3,3,3,3,4} Steritruncated 6-orthoplex Cellitruncated hexacontatetrapeton (catog)
27								t0,2,4{3,3,3,3,4} Stericantellated 6-orthoplex Cellirhombated hexacontatetrapeton (crag)
28								t1,2,4{3,3,3,3,4} Biruncitruncated 6-orthoplex Biprismatotruncated hexacontatetrapeton (boprax)
29								t0,3,4{3,3,3,3,4} Steriruncinated 6-orthoplex Celliprismated hexacontatetrapeton (copog)
30								t1,2,4{4,3,3,3,3} Biruncitruncated 6-cube Biprismatotruncated hexeract (boprag)
31								t1,2,3{4,3,3,3,3} Bicantitruncated 6-cube Great birhombated hexeract (gaborx)
32								t0,1,5{3,3,3,3,4} Pentitruncated 6-orthoplex Teritruncated hexacontatetrapeton (tacox)
33								t0,2,5{3,3,3,3,4} Penticantellated 6-orthoplex Terirhombated hexacontatetrapeton (tapox)
34								t0,3,4{4,3,3,3,3} Steriruncinated 6-cube Celliprismated hexeract (copox)
35								t0,2,5{4,3,3,3,3} Penticantellated 6-cube Terirhombated hexeract (topag)
36								t0,2,4{4,3,3,3,3} Stericantellated 6-cube Cellirhombated hexeract (crax)
37								t0,2,3{4,3,3,3,3} Runcicantellated 6-cube Prismatorhombated hexeract (prox)
38								t0,1,5{4,3,3,3,3} Pentitruncated 6-cube Teritruncated hexeract (tacog)
39								t0,1,4{4,3,3,3,3} Steritruncated 6-cube Cellitruncated hexeract (catax)
40								t0,1,3{4,3,3,3,3} Runcitruncated 6-cube Prismatotruncated hexeract (potax)
41								t0,1,2{4,3,3,3,3} Cantitruncated 6-cube Great rhombated hexeract (grox)
42								t0,1,2,3{3,3,3,3,4} Runcicantitruncated 6-orthoplex Great prismated hexacontatetrapeton (gopog)
43								t0,1,2,4{3,3,3,3,4} Stericantitruncated 6-orthoplex Celligreatorhombated hexacontatetrapeton (cagorg)
44								t0,1,3,4{3,3,3,3,4} Steriruncitruncated 6-orthoplex Celliprismatotruncated hexacontatetrapeton (captog)
45								t0,2,3,4{3,3,3,3,4} Steriruncicantellated 6-orthoplex Celliprismatorhombated hexacontatetrapeton (coprag)
46								t1,2,3,4{4,3,3,3,3} Biruncicantitruncated 6-cube Great biprismato-hexeractihexacontitetrapeton (gobpoxog)
47								t0,1,2,5{3,3,3,3,4} Penticantitruncated 6-orthoplex Terigreatorhombated hexacontatetrapeton (togrig)
48								t0,1,3,5{3,3,3,3,4} Pentiruncitruncated 6-orthoplex Teriprismatotruncated hexacontatetrapeton (tocrax)
49								t0,2,3,5{4,3,3,3,3} Pentiruncicantellated 6-cube Teriprismatorhombi-hexeractihexacontitetrapeton (tiprixog)
50								t0,2,3,4{4,3,3,3,3} Steriruncicantellated 6-cube Celliprismatorhombated hexeract (coprix)
51								t0,1,4,5{4,3,3,3,3} Pentisteritruncated 6-cube Tericelli-hexeractihexacontitetrapeton (tactaxog)
52								t0,1,3,5{4,3,3,3,3} Pentiruncitruncated 6-cube Teriprismatotruncated hexeract (tocrag)
53								t0,1,3,4{4,3,3,3,3} Steriruncitruncated 6-cube Celliprismatotruncated hexeract (captix)
54								t0,1,2,5{4,3,3,3,3} Penticantitruncated 6-cube Terigreatorhombated hexeract (togrix)
55								t0,1,2,4{4,3,3,3,3} Stericantitruncated 6-cube Celligreatorhombated hexeract (cagorx)
56								t0,1,2,3{4,3,3,3,3} Runcicantitruncated 6-cube Great prismated hexeract (gippox)
57								t0,1,2,3,4{3,3,3,3,4} Steriruncicantitruncated 6-orthoplex Great cellated hexacontatetrapeton (gocog)
58								t0,1,2,3,5{3,3,3,3,4} Pentiruncicantitruncated 6-orthoplex Terigreatoprismated hexacontatetrapeton (tagpog)
59								t0,1,2,4,5{3,3,3,3,4} Pentistericantitruncated 6-orthoplex Tericelligreatorhombated hexacontatetrapeton (tecagorg)
60								t0,1,2,4,5{4,3,3,3,3} Pentistericantitruncated 6-cube Tericelligreatorhombated hexeract (tocagrax)
61								t0,1,2,3,5{4,3,3,3,3} Pentiruncicantitruncated 6-cube Terigreatoprismated hexeract (tagpox)
62								t0,1,2,3,4{4,3,3,3,3} Steriruncicantitruncated 6-cube Great cellated hexeract (gocax)
63								t0,1,2,3,4,5{4,3,3,3,3} Omnitruncated 6-cube Great teri-hexeractihexacontitetrapeton (gotaxog)

References

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
• Klitzing, Richard. "6D uniform polytopes (polypeta)".