Wikipedia

Transonic

(Redirected from Transsonic)

For the American company, see Transonic Combustion.

Transonic (or transsonic) flow is air flowing around an object at a speed that generates regions of both subsonic and supersonic airflow around that object.[1] The exact range of speeds depends on the object's critical Mach number, but transonic flow is seen at flight speeds close to the speed of sound (343 m/s at sea level), typically between Mach 0.8 and 1.2.[1]

Aerodynamic condensation evidences of supersonic expansion fans around a transonic F/A-18
The Sears–Haack body presents a cross-sectional area variation that minimises wave drag.
Shock waves may appear as weak optical disturbances above airliners with supercritical wings
Transonic flow patterns on an airfoil showing flow patterns at and above critical Mach number

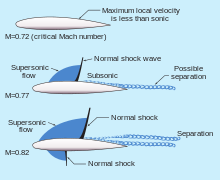
The issue of transonic speed (or transonic region) first appeared during World War II.[2] Pilots found as they approached the sound barrier the airflow caused aircraft to become unsteady.[2] Experts found that shock waves can cause large-scale separation downstream, increasing drag, adding asymmetry and unsteadiness to the flow around the vehicle.[3] Research has been done into weakening shock waves in transonic flight through the use of anti-shock bodies and supercritical airfoils.[3]

Most modern jet powered aircraft are engineered to operate at transonic air speeds.[4] Transonic airspeeds see a rapid increase in drag from about Mach 0.8, and it is the fuel costs of the drag that typically limits the airspeed. Attempts to reduce wave drag can be seen on all high-speed aircraft. Most notable is the use of swept wings, but another common form is a wasp-waist fuselage as a side effect of the Whitcomb area rule.

Transonic speeds can also occur at the tips of rotor blades of helicopters and aircraft. This puts severe, unequal stresses on the rotor blade and may lead to accidents if it occurs. It is one of the limiting factors of the size of rotors and the forward speeds of helicopters (as this speed is added to the forward-sweeping [leading] side of the rotor, possibly causing localized transonics).

History

edit

Discovering transonic airflow

edit

Issues with aircraft flight relating to speed first appeared during the supersonic era in 1941.[5] Ralph Virden, a test pilot, crashed in a fatal plane accident.[6] He lost control of the plane when a shock wave caused by supersonic airflow developed over the wing, causing it to stall.[6] Virden flew well below the speed of sound at Mach 0.675, which brought forth the idea of different airflows forming around the plane.[5] In the 40s, Kelly Johnson became one of the first engineers to investigate the effect of compressibility on aircraft.[5] However, contemporary wind tunnels did not have the capability to create wind speeds close to Mach 1 to test the effects of transonic speeds.[6] Not long after, the term "transonic" was defined to mean "across the speed of sound" and was invented by NACA director Hugh Dryden and Theodore von Kármán of the California Institute of Technology.[5]

Changes in aircraft

edit

Initially, NACA designed "dive flaps" to help stabilize the plane when reaching transonic flight.[5] This small flap on the underside of the plane slowed the plane to prevent shock waves, but this design only delayed finding a solution to aircraft flying at supersonic speed.[5] Newer wind tunnels were designed, so researchers could test newer wing designs without risking test pilots' lives.[7] The slotted-wall transonic tunnel was designed by NASA and allowed researchers to test wings and different airfoils in transonic airflow to find the best wingtip shape for sonic speeds.[7]

After World War II, major changes in aircraft design were seen to improve transonic flight.[6] The main way to stabilize an aircraft was to reduce the speed of the airflow around the wings by changing the chord of the plane wings, and one solution to prevent transonic waves was swept wings.[5] Since the airflow would hit the wings at an angle, this would decrease the wing thickness and chord ratio.[5] Airfoils wing shapes were designed flatter at the top to prevent shock waves and reduce the distance of airflow over the wing.[8] Later on, Richard Whitcomb designed the first supercritical airfoil using similar principles.[7]

Mathematical analysis

edit
 
Streamlines for three airflow regimes (black lines) around a nondescript blunt body (blue).[9]

Prior to the advent of powerful computers, even the simplest forms of the compressible flow equations were difficult to solve due to their nonlinearity.[6] A common assumption used to circumvent this nonlinearity is that disturbances within the flow are relatively small, which allows mathematicians and engineers to linearize the compressible flow equations into a relatively easily solvable set of differential equations for either wholly subsonic or supersonic flows.[6] This assumption is fundamentally untrue for transonic flows because the disturbance caused by an object is much larger than in subsonic or supersonic flows; a flow speed close to or at Mach 1 does not allow the streamtubes (3D flow paths) to contract enough around the object to minimize the disturbance, and thus the disturbance propagates.[9] Aerodynamicists struggled during the earlier studies of transonic flow because the then-current theory implied that these disturbances– and thus drag– approached infinity as local Mach number approached 1, an obviously unrealistic result which could not be remedied using known methods.[6]

One of the first methods used to circumvent the nonlinearity of transonic flow models was the hodograph transformation.[2] This concept was originally explored in 1923 by an Italian mathematician named Francesco Tricomi, who used the transformation to simplify the compressible flow equations and prove that they were solvable.[2] The hodograph transformation itself was also explored by both Ludwig Prandtl and O.G. Tietjen's textbooks in 1929 and by Adolf Busemann in 1937, though neither applied this method specifically to transonic flow.[2]

Gottfried Guderley, a German mathematician and engineer at Braunschweig, discovered Tricomi's work in the process of applying the hodograph method to transonic flow near the end of World War II.[2] He focused on the nonlinear thin-airfoil compressible flow equations, the same as what Tricomi derived, though his goal of using these equations to solve flow over an airfoil presented unique challenges.[2][6] Guderley and Hideo Yoshihara, along with some input from Busemann, later used a singular solution of Tricomi's equations to analytically solve the behavior of transonic flow over a double wedge airfoil, the first to do so with only the assumptions of thin-airfoil theory.[2][6]

Although successful, Guderley's work was still focused on the theoretical, and only resulted in a single solution for a double wedge airfoil at Mach 1.[2] Walter Vincenti, an American engineer at Ames Laboratory, aimed to supplement Guderley's Mach 1 work with numerical solutions that would cover the range of transonic speeds between Mach 1 and wholly supersonic flow.[2] Vincenti and his assistants drew upon the work of Howard Emmons as well as Tricomi's original equations to complete a set of four numerical solutions for the drag over a double wedge airfoil in transonic flow above Mach 1.[2] The gap between subsonic and Mach 1 flow was later covered by both Julian Cole and Leon Trilling, completing the transonic behavior of the airfoil by the early 1950s.[2]

Condensation clouds

edit

At transonic speeds supersonic expansion fans form intense low-pressure, low-temperature areas at various points around an aircraft. If the temperature drops below the dew point a visible cloud will form. These clouds remain with the aircraft as it travels. It is not necessary for the aircraft as a whole to reach supersonic speeds for these clouds to form. Typically, the tail of the aircraft will reach supersonic flight while the nose of the aircraft is still in subsonic flight. A bubble of supersonic expansion fans terminating by a wake shockwave surround the tail. As the aircraft continues to accelerate, the supersonic expansion fans will intensify and the wake shockwave will grow in size until infinity is reached, at which point the bow shockwave forms. This is Mach 1 and the Prandtl–Glauert singularity.

Transonic flows in astronomy and astrophysics

edit

In astrophysics, wherever there is evidence of shocks (standing, propagating or oscillating), the flow close by must be transonic, as only supersonic flows form shocks. All black hole accretions are transonic.[10] Many such flows also have shocks very close to the black holes.

The outflows or jets from young stellar objects or disks around black holes can also be transonic since they start subsonically and at a far distance they are invariably supersonic. Supernovae explosions are accompanied by supersonic flows and shock waves. Bow shocks formed in solar winds are a direct result of transonic winds from a star. It had been long thought that a bow shock was present around the heliosphere of our solar system, but this was found not to be the case according to IBEX data published in 2012.[11]

See also

edit
 
Look up transonic in Wiktionary, the free dictionary.

References

edit
  1. ^ a b Anderson, John D. Jr. (2017). Fundamentals of aerodynamics (Sixth ed.). New York, NY. pp. 756–758. ISBN 978-1-259-12991-9. OCLC 927104254.{{cite book}}: CS1 maint: location missing publisher (link)
  2. ^ a b c d e f g h i j k l Vincenti, Walter G.; Bloor, David (August 2003). "Boundaries, Contingencies and Rigor". Social Studies of Science. 33 (4): 469–507. doi:10.1177/0306312703334001. ISSN 0306-3127. S2CID 13011496.
  3. ^ a b Takahashi, Timothy (15 December 2017). Aircraft performance and sizing. fundamentals of aircraft performance. Momentum Press. p. 107. ISBN 978-1-60650-684-4. OCLC 1162468861.
  4. ^ Takahashi, Timothy (2016). Aircraft Performance and Sizing, Volume I. New York City: Momentum Press Engineering. pp. 10–11. ISBN 978-1-60650-683-7.
  5. ^ a b c d e f g h "Mach 1: Assaulting the Barrier". Air & Space Magazine. Retrieved 14 March 2021.
  6. ^ a b c d e f g h i Vincenti, Walter G. (1997). Engineering theory in the making: Aerodynamic calculation "breaks the sound barrier.". OCLC 1027014606.
  7. ^ a b c "From Engineering Science to Big Science: The NACA and NASA Collier Trophy Research Project Winners. Pamela E. Mack". Isis. 91 (2): 417–418. 2000–2006. doi:10.1086/384834. ISSN 0021-1753.
  8. ^ Hicks, Raymond M.; Vanderplaats, Garret N.; Murman, Earll M.; King, Rosa R. (1 February 1976). "Airfoil Section Drag Reduction at Transonic Speeds by Numerical Optimization". SAE Technical Paper Series. 1. Warrendale, PA: SAE International. doi:10.4271/760477. hdl:2060/19760009938. S2CID 118185921.
  9. ^ a b Ramm, Heinrich J. (1990). Fluid dynamics for the study of transonic flow. New York: Oxford University Press. ISBN 1-60129-748-3. OCLC 228117297.
  10. ^ Chakrabarti, Sandip (1990). Theory of Transonic Astrophysical Flows. Singapore: World Scientific. ISBN 981-02-0204-0.
  11. ^ "NASA – IBEX Reveals a Missing Boundary At the Edge of the Solar System", Science daily, 10 May 2012.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Transonic&oldid=1255285722"